Admin (обсуждение | вклад) (→Основные параметры и принципы расчета KAMA) |
Admin (обсуждение | вклад) |
||
| (не показаны 2 промежуточных версий 1 участника) | |||
| Строка 1: | Строка 1: | ||
| − | '''Адаптивная скользящая средняя Кауфмана (KAMA)''' - это индикатор, рассчитывающий средние значения | + | '''Адаптивная скользящая средняя Кауфмана (KAMA)''' - это индикатор, рассчитывающий средние значения [[Таймфрейм|таймфреймов]] по динамично изменяющемуся значению периода в пределах настроек, заданных пользователем. |
| − | Скользящая средняя - один из ряда первых индикаторов, возникший после того, как ценовые колебания были сформированы во временные диапазоны. Такие формации (свечи, бары) подразумевали конкретные идентификационные значения (цена открытия, закрытия, экстремумы), что позволило использовать их в расчетах формул индикаторов для технического анализа рынка. Естественно, что одной из первых идей было усреднение значения свеч. Так появилась скользящая средняя. | + | [[Moving Averages|Скользящая средняя]] - один из ряда первых индикаторов, возникший после того, как ценовые колебания были сформированы во временные диапазоны. Такие формации ([[Японские свечи|свечи]], бары) подразумевали конкретные идентификационные значения (цена открытия, закрытия, экстремумы), что позволило использовать их в расчетах формул индикаторов для технического анализа рынка. Естественно, что одной из первых идей было усреднение значения свеч. Так появилась скользящая средняя. |
Новаторство и упорство внедрения скользящих средних приписывается Ричарду Доничини и Херсту. Помимо скользящей средней обычной, просто усредняющей цены закрытия диапазона, была создана экспоненциальная, использующая коэффициент, утяжеляющий недавние значения цены, ей вторила по аналогии придачи веса ближним значениям сглаженная и линейно взвешенная, в которой сам весовой коэффициент изменялся по линейному закону. | Новаторство и упорство внедрения скользящих средних приписывается Ричарду Доничини и Херсту. Помимо скользящей средней обычной, просто усредняющей цены закрытия диапазона, была создана экспоненциальная, использующая коэффициент, утяжеляющий недавние значения цены, ей вторила по аналогии придачи веса ближним значениям сглаженная и линейно взвешенная, в которой сам весовой коэффициент изменялся по линейному закону. | ||
| Строка 17: | Строка 17: | ||
За основу Кауфманом была взята экспоненциальная скользящая средняя. Используя ее классическую формулу: | За основу Кауфманом была взята экспоненциальная скользящая средняя. Используя ее классическую формулу: | ||
| − | EMA = к*Цена закрытия + (1-к) ЕМА предыдущая, но расчет коэффициента к производился исходя из предпосылок, предложенных и использованных Тушаром Шонде по внедрению динамического изменяющегося параметра коэффициента периода скользящей в зависимости от величины волатильности. | + | EMA = к*Цена закрытия + (1-к) ЕМА предыдущая, но расчет коэффициента к производился исходя из предпосылок, предложенных и использованных Тушаром Шонде по внедрению динамического изменяющегося параметра коэффициента периода скользящей в зависимости от величины [[Волатильность|волатильности]]. |
В стандартном виде исчисления ЕМА сам коэффициент к считается как: к=2/(n+1), | В стандартном виде исчисления ЕМА сам коэффициент к считается как: к=2/(n+1), | ||
| Строка 29: | Строка 29: | ||
При росте «размаха» цен такая скользящая будет вплотную прижиматься к графику, оперативно реагируя на любые изменения, тогда как при флэте скользящая будет «отдалятся» от графика, уменьшая тем самым количество возможных пересечений, а значит, и ложных сигналов. | При росте «размаха» цен такая скользящая будет вплотную прижиматься к графику, оперативно реагируя на любые изменения, тогда как при флэте скользящая будет «отдалятся» от графика, уменьшая тем самым количество возможных пересечений, а значит, и ложных сигналов. | ||
| − | Кауфман пошел практически по тому же пути. Он ввел понятие «Сигнал». Если мы возьмем некий период скользящей средней, отнимем начальную и конечную цену этого периода, взяв разницу по модулю (чтобы знак не имел значения в расчетах), то мы можем говорить, что на данном рассматриваемом промежутке имеет место некий числовой сигнал или, говоря другими словами, | + | Кауфман пошел практически по тому же пути. Он ввел понятие «Сигнал». Если мы возьмем некий период скользящей средней, отнимем начальную и конечную цену этого периода, взяв разницу по модулю (чтобы знак не имел значения в расчетах), то мы можем говорить, что на данном рассматриваемом промежутке имеет место некий числовой сигнал или, говоря другими словами, [[Momentum|Momentum]]. |
Определив этот диапазон как Сигнал = Цена конца периода - Цена начала периода, Кауфман решил отсеять шумы цены на этом диапазоне, складывая абсолютные значения диапазона каждой свечи разности типа ∑ разниц диапазонов = ( │Цена закрытия второго таймфрема - Ценазакрытия первого таймфрейма│) + …..(│Цена закрытия последнего тймфрема - Цена закрытия предпоследнего тймфрема│) | Определив этот диапазон как Сигнал = Цена конца периода - Цена начала периода, Кауфман решил отсеять шумы цены на этом диапазоне, складывая абсолютные значения диапазона каждой свечи разности типа ∑ разниц диапазонов = ( │Цена закрытия второго таймфрема - Ценазакрытия первого таймфрейма│) + …..(│Цена закрытия последнего тймфрема - Цена закрытия предпоследнего тймфрема│) | ||
| Строка 35: | Строка 35: | ||
Соотношение сигнала к сумме шумов сам автор назвал «Коэффициентом Эффективности» (ER в англоязычной версии). | Соотношение сигнала к сумме шумов сам автор назвал «Коэффициентом Эффективности» (ER в англоязычной версии). | ||
| − | Коэффициент эффективности = Сигнал/∑разниц диапазонов. Исходя из компонентов такого соотношения, результирующие значения могут начинаться с нуля и заканчиваться единицей, причем при наличии тренда, он будет стремиться к 1, тогда как при флэтах падать к нулевым значениям. | + | Коэффициент эффективности = Сигнал/∑разниц диапазонов. Исходя из компонентов такого соотношения, результирующие значения могут начинаться с нуля и заканчиваться единицей, причем при наличии тренда, он будет стремиться к 1, тогда как при [[Флэт (Flat)|флэтах]] падать к нулевым значениям. |
После решения задачи по автоматическому выбору диапазона с помощью ER (увеличение или уменьшение диапазона, в зависимости от возрастания или убывания силы шумов), автор приступил к поиску коэффициента сглаживания, который бы позволил выбирать «режимы» для скользящей средней, соблюдая адаптацию в зависимости от скорости изменения последних данных котировок. | После решения задачи по автоматическому выбору диапазона с помощью ER (увеличение или уменьшение диапазона, в зависимости от возрастания или убывания силы шумов), автор приступил к поиску коэффициента сглаживания, который бы позволил выбирать «режимы» для скользящей средней, соблюдая адаптацию в зависимости от скорости изменения последних данных котировок. | ||
| Строка 93: | Строка 93: | ||
Фильтр = | Фильтр = | ||
| − | , где | + | [[Файл:KAMA_101.png]], где |
| − | , то есть математическое ожидание за период d (равный 10 по умолчанию). | + | [[Файл:KAMA_102.png]], то есть математическое ожидание за период d (равный 10 по умолчанию). |
Коэффициент К в формуле фильтра является процентным коэффициентом. По поводу выбора величины К автор говорил о том, что он должен быть пропорционален рычагу плеча, используемого для торгового актива, то есть для фьючерсов, торгуемых с плечом 10 значение коэффициента предлагалось брать 0,1, тогда как для акций у них плечо отсутствует вовсе (плечи используются только в деривативах, размер их можно найти в описании спецификации прилагаемой к каждому контракту) – единицу (100%). | Коэффициент К в формуле фильтра является процентным коэффициентом. По поводу выбора величины К автор говорил о том, что он должен быть пропорционален рычагу плеча, используемого для торгового актива, то есть для фьючерсов, торгуемых с плечом 10 значение коэффициента предлагалось брать 0,1, тогда как для акций у них плечо отсутствует вовсе (плечи используются только в деривативах, размер их можно найти в описании спецификации прилагаемой к каждому контракту) – единицу (100%). | ||
| Строка 111: | Строка 111: | ||
Благодаря вводу данного фильтра, часть сделок на боковике (движение актива, которое не превышает некий сложившийся и визуально наблюдаемый диапазон) уйдет, что позволит поднять эффективность индикатора КАМА. | Благодаря вводу данного фильтра, часть сделок на боковике (движение актива, которое не превышает некий сложившийся и визуально наблюдаемый диапазон) уйдет, что позволит поднять эффективность индикатора КАМА. | ||
| − | Необходимо отметить, что именно благодаря Кауфману в трейдинг был введен прием по использованию среднеквадратичных отклонений, которые используют по сей день во многих новых индикаторах, в частности, в самом известном индикаторе лент Боллинджера. | + | Необходимо отметить, что именно благодаря Кауфману в трейдинг был введен прием по использованию среднеквадратичных отклонений, которые используют по сей день во многих новых индикаторах, в частности, в самом известном индикаторе лент [[Bollinger Bands|Боллинджера]]. |
[[Файл:KAMA_12.jpg|border|1000x400px]] | [[Файл:KAMA_12.jpg|border|1000x400px]] | ||
| Строка 119: | Строка 119: | ||
Сложность расчета того или иного индикатора не может служить залогом прибыльности стратегии на нем основанной. Всегда предпочтительно использование индикаторов в совокупности, учитывая особенности каждого по отдельности. Один индикатор эффективен при трендовых движениях, второй при нахождении рынка во флэта, третий помогает правильной и «экономной» постановке стопов. | Сложность расчета того или иного индикатора не может служить залогом прибыльности стратегии на нем основанной. Всегда предпочтительно использование индикаторов в совокупности, учитывая особенности каждого по отдельности. Один индикатор эффективен при трендовых движениях, второй при нахождении рынка во флэта, третий помогает правильной и «экономной» постановке стопов. | ||
| − | Какой путь к верстке стратегии был ни выбран, простой или сложный, с одним индикатором или со многими, всегда важно соблюдать одно условие - тестирование стратегии на исторических данных до начала торгов. Чтобы погрешность была минимальной, не возникало нестандартных, вне тестовых ситуаций при реальной торговле, историческую выборку для теста надо готовить с включением в нее всех примеров возможных состояний рынка: флэтов, трендов, высоковолатильных участков. | + | Какой путь к верстке стратегии был ни выбран, простой или сложный, с одним индикатором или со многими, всегда важно соблюдать одно условие - тестирование стратегии на исторических данных до начала торгов. Чтобы погрешность была минимальной, не возникало нестандартных, вне тестовых ситуаций при реальной торговле, историческую выборку для теста надо готовить с включением в нее всех примеров возможных состояний рынка: флэтов, трендов, [[Ликвидность|высоковолатильных]] участков. |
Нельзя не отметить, что если вы открыли для себя страницу адаптивных скользящих средних, значит, вы сделали шаг в мир применения фильтрации шумов и адаптирования рыночных данных с использованием сложных методов, начиная от формул, используемых для космической навигации и наземной связи до "черных ящиков" Jrik Research - формул расчетов скользящих, которые держатся в строжайшем секрете. | Нельзя не отметить, что если вы открыли для себя страницу адаптивных скользящих средних, значит, вы сделали шаг в мир применения фильтрации шумов и адаптирования рыночных данных с использованием сложных методов, начиная от формул, используемых для космической навигации и наземной связи до "черных ящиков" Jrik Research - формул расчетов скользящих, которые держатся в строжайшем секрете. | ||
| Строка 126: | Строка 126: | ||
[[Медиа:KAMA.mq4]] | [[Медиа:KAMA.mq4]] | ||
| + | |||
| + | [[Category:Трендовые индикаторы]] | ||
| + | [[Category:Индикаторы]] | ||
| + | [[Category:Термины]] | ||
Текущая версия на 13:49, 9 августа 2016
Адаптивная скользящая средняя Кауфмана (KAMA) - это индикатор, рассчитывающий средние значения таймфреймов по динамично изменяющемуся значению периода в пределах настроек, заданных пользователем.
Скользящая средняя - один из ряда первых индикаторов, возникший после того, как ценовые колебания были сформированы во временные диапазоны. Такие формации (свечи, бары) подразумевали конкретные идентификационные значения (цена открытия, закрытия, экстремумы), что позволило использовать их в расчетах формул индикаторов для технического анализа рынка. Естественно, что одной из первых идей было усреднение значения свеч. Так появилась скользящая средняя.
Новаторство и упорство внедрения скользящих средних приписывается Ричарду Доничини и Херсту. Помимо скользящей средней обычной, просто усредняющей цены закрытия диапазона, была создана экспоненциальная, использующая коэффициент, утяжеляющий недавние значения цены, ей вторила по аналогии придачи веса ближним значениям сглаженная и линейно взвешенная, в которой сам весовой коэффициент изменялся по линейному закону.
Чтобы доказать преимущество, достоинство или недостатки того или иного вида скользящей средней, тратились годы тестов (Хокхаймер - «Компьютеры помогут вам в игре на фьючерсных играх»), писались многочисленные труды (Ч.Лебо и Д.Лукас), испытывались различные подходы (Нэйман, ДеМарк, Эдлер).
В спорах, которые велись, выявилась проблематика выбора периода скользящей средней, потому как косвенно значение данного параметра влияло на запаздывание отклика индикатора на динамику цены актива.
В 1995 году Перри Кауфман предложил свое решение данной проблемы.
Содержание
Основные параметры и принципы расчета KAMA
За основу Кауфманом была взята экспоненциальная скользящая средняя. Используя ее классическую формулу:
EMA = к*Цена закрытия + (1-к) ЕМА предыдущая, но расчет коэффициента к производился исходя из предпосылок, предложенных и использованных Тушаром Шонде по внедрению динамического изменяющегося параметра коэффициента периода скользящей в зависимости от величины волатильности.
В стандартном виде исчисления ЕМА сам коэффициент к считается как: к=2/(n+1),
n - является периодом скользящей средней. Тушар Шонде сделал значения коэффициента к динамичным, представив формулу расчета коэффициента как произведение осциллятора, который разработал сам. Chande Momentum Oscilator умноженное на коэффициент (к*СМО).
Скользящую Тушар Шонде назвал –
VIDYA (Variable Index Dynamic Average) = к*СМО*Цена закрытия +(1-к*СМО)ЕМА предыдущая
При росте «размаха» цен такая скользящая будет вплотную прижиматься к графику, оперативно реагируя на любые изменения, тогда как при флэте скользящая будет «отдалятся» от графика, уменьшая тем самым количество возможных пересечений, а значит, и ложных сигналов.
Кауфман пошел практически по тому же пути. Он ввел понятие «Сигнал». Если мы возьмем некий период скользящей средней, отнимем начальную и конечную цену этого периода, взяв разницу по модулю (чтобы знак не имел значения в расчетах), то мы можем говорить, что на данном рассматриваемом промежутке имеет место некий числовой сигнал или, говоря другими словами, Momentum.
Определив этот диапазон как Сигнал = Цена конца периода - Цена начала периода, Кауфман решил отсеять шумы цены на этом диапазоне, складывая абсолютные значения диапазона каждой свечи разности типа ∑ разниц диапазонов = ( │Цена закрытия второго таймфрема - Ценазакрытия первого таймфрейма│) + …..(│Цена закрытия последнего тймфрема - Цена закрытия предпоследнего тймфрема│)
Соотношение сигнала к сумме шумов сам автор назвал «Коэффициентом Эффективности» (ER в англоязычной версии).
Коэффициент эффективности = Сигнал/∑разниц диапазонов. Исходя из компонентов такого соотношения, результирующие значения могут начинаться с нуля и заканчиваться единицей, причем при наличии тренда, он будет стремиться к 1, тогда как при флэтах падать к нулевым значениям.
После решения задачи по автоматическому выбору диапазона с помощью ER (увеличение или уменьшение диапазона, в зависимости от возрастания или убывания силы шумов), автор приступил к поиску коэффициента сглаживания, который бы позволил выбирать «режимы» для скользящей средней, соблюдая адаптацию в зависимости от скорости изменения последних данных котировок.
Для расчета данного коэффициента Кауфман воплотил идею ввести две константы, которые рассчитывались по классическим формулам расчета стандартного коэффициента ЕМА
но быстрая константа имела период равный по умолчанию двум, а медленная имела период 30.
Тогда в стандартном варианте мы имеем следующие значения констант.
Быстрая сглаживающая константа Fast Smoothing Constant = 2/(2+1) = 0.6667
Медленная сглаживающая константа Slow Smoothing Constant = 2/(30+1) = 0.06456667
Сам коэффициент сглаживания Кауфман представил в виде следующей формулы:
Scaled Smoothing Constant = ER (Быстрая константа - Медленная константа) + Медленная
Вот, наконец-то готова формула расчета коэффициента Кауфмана для КАМА:
К = (Scaled Smoothing Constant)^2, то есть возведенному в квадрат коэффициенту сглаживания. Сама же формула адаптированной скользящей средней выглядит точно так же как и ЕМА:
КАМА = К*Цена закрытия + (1-К) КАМАпредыдущая
Стратегии основанные на использовании КАМА
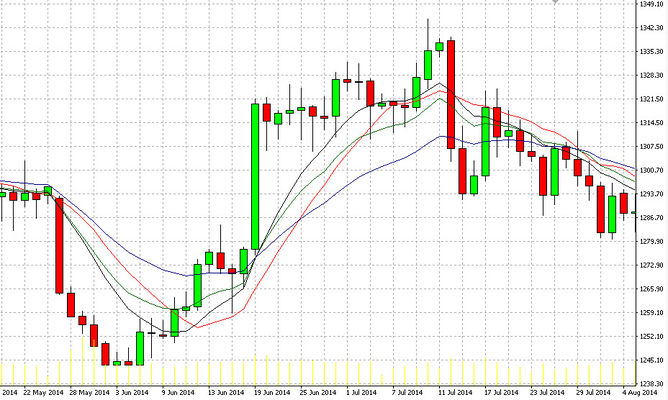
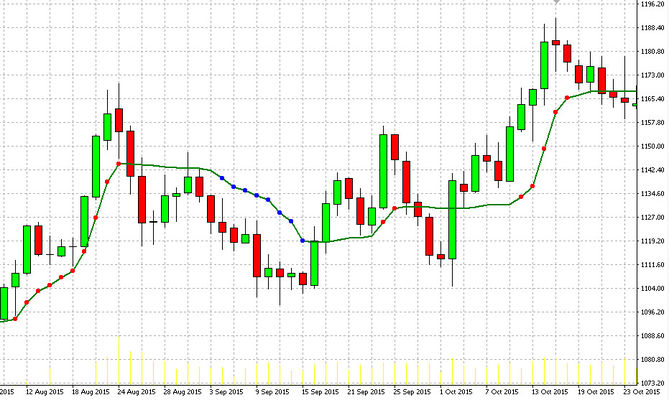
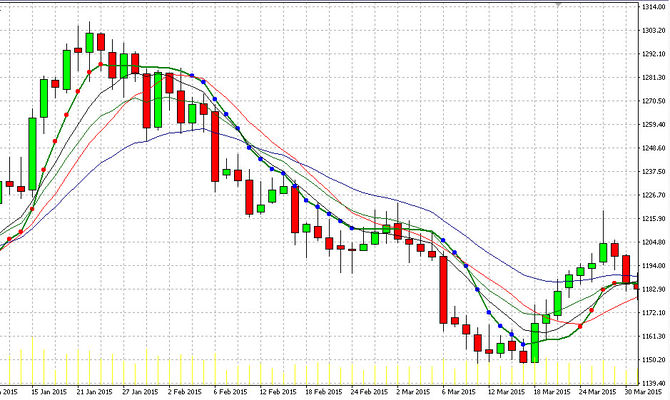
Насколько был сложен вывод, настолько просты правила стратегии. КАМА, несмотря на сложность, всего лишь скользящая средняя. На графике присутствует только цена актива и КАМА.
Входы сами по себе просты: если котировка пересекает КАМА сверху и закрывается ниже (можно допустить несколько закрытий, если выбран малый таймфрейм), то мы имеем сигнал на продажу для анализируемого инструмента. Надо особо отметить, что из-за особенностей расчетов при таком пресечении происходит разворот и самой кривой КАМА.
Закрытие цены свечи выше кривой линии КАМА (или несколько закрытий, если выбран малый таймфрейм) говорит о возникновении сигнала на покупку анализируемого инструмента.
Надо сказать, что обычно такие стратегии предусматривают реверсивное исполнение. То есть, трейдер все время в рынке или говорят «все время в позиции», при возникновении противоположного сигнала, закрывается предыдущая позиция и открывается новая.
Авторские значения параметров и замечания
Как нами было выше описано, при вычислении значения быстрой и медленной константы сглаживания применяются значения 2 и 30, в оригинальных настройках они обозначаются латинскими буквами f,s
F=2
S=30
N=10 - это значение выбрано автором как окно для поиска тренда, при вычислении значения «Сигнала» для ER. На этой же выборке из таймфремов определяется волатильность.
Сам автор указывал на то, что при использовании КАМА, необходимо применять фильтрацию для того, чтобы отсеять ложные сигналы.
Расчет фильтра автор предложил производить используя среднеквадратичное отклонение ежедневных диапазонов изменения КАМА (если допустим, что у нас настроен дневной таймфрейм). То есть:
КАМА сегодняшнего таймфрема - КАМА предыдущего таймфрема
Период, за который берутся эти приращения равен 10, то есть ровно такой же, как и период самой КАМА.
Фильтр =
![]() , то есть математическое ожидание за период d (равный 10 по умолчанию).
, то есть математическое ожидание за период d (равный 10 по умолчанию).
Коэффициент К в формуле фильтра является процентным коэффициентом. По поводу выбора величины К автор говорил о том, что он должен быть пропорционален рычагу плеча, используемого для торгового актива, то есть для фьючерсов, торгуемых с плечом 10 значение коэффициента предлагалось брать 0,1, тогда как для акций у них плечо отсутствует вовсе (плечи используются только в деривативах, размер их можно найти в описании спецификации прилагаемой к каждому контракту) – единицу (100%).
При использовании фильтров стратегия преображается в следующую форму с новыми уточняющими условиями:
При входе в позицию покупки актива, сравнивают разницу текущего и наименьшего значения
КАМА текущее значение - КАМА мин ≥ Фильтр, если условие выполняется, тогда можно производить покупку.
Для продаж нам также необходимо сравнить разницу текущего и максимума с пороговым значением Фильтра
Фильтр ≤ КАМА макс - КАМА текущее значение;
Благодаря вводу данного фильтра, часть сделок на боковике (движение актива, которое не превышает некий сложившийся и визуально наблюдаемый диапазон) уйдет, что позволит поднять эффективность индикатора КАМА.
Необходимо отметить, что именно благодаря Кауфману в трейдинг был введен прием по использованию среднеквадратичных отклонений, которые используют по сей день во многих новых индикаторах, в частности, в самом известном индикаторе лент Боллинджера.
Выводы
Сложность расчета того или иного индикатора не может служить залогом прибыльности стратегии на нем основанной. Всегда предпочтительно использование индикаторов в совокупности, учитывая особенности каждого по отдельности. Один индикатор эффективен при трендовых движениях, второй при нахождении рынка во флэта, третий помогает правильной и «экономной» постановке стопов.
Какой путь к верстке стратегии был ни выбран, простой или сложный, с одним индикатором или со многими, всегда важно соблюдать одно условие - тестирование стратегии на исторических данных до начала торгов. Чтобы погрешность была минимальной, не возникало нестандартных, вне тестовых ситуаций при реальной торговле, историческую выборку для теста надо готовить с включением в нее всех примеров возможных состояний рынка: флэтов, трендов, высоковолатильных участков.
Нельзя не отметить, что если вы открыли для себя страницу адаптивных скользящих средних, значит, вы сделали шаг в мир применения фильтрации шумов и адаптирования рыночных данных с использованием сложных методов, начиная от формул, используемых для космической навигации и наземной связи до "черных ящиков" Jrik Research - формул расчетов скользящих, которые держатся в строжайшем секрете.