Admin (обсуждение | вклад) |
Admin (обсуждение | вклад) |
||
| (не показана 1 промежуточная версия 1 участника) | |||
| Строка 1: | Строка 1: | ||
| − | '''Фрактальная адаптивная скользящая средняя (FRAMA)''' - индикатор, адаптирующий свою скорость изменения исчисления, исходя из скорости изменения котировок. | + | '''Фрактальная адаптивная скользящая средняя (FRAMA)''' - индикатор, адаптирующий свою скорость изменения исчисления, исходя из скорости изменения [[Котировка|котировок]]. |
Начало 90-х годов прошлого века означилось прорывом в области адаптаций рыночных областей значений анализируемых инструментов к соответствию динамики изменяющихся состояний рынка. | Начало 90-х годов прошлого века означилось прорывом в области адаптаций рыночных областей значений анализируемых инструментов к соответствию динамики изменяющихся состояний рынка. | ||
| − | Для технического анализа рынка используются индикаторы, в расчетах которых используются входные данные, выдаваемые временными интервалами и сгруппированными на этих интервалах значениями котировок. Наиболее распространенная и общепринятая группировка котировок - в виде свечей или баров. Выделяют 3 вида данных получаемых от свечной конфигурации или баров: цена, по которой был открыт период; цена, по которой период был закрыт; экстремальные значения данного временного периода. | + | Для [[Технический анализ|технического анализа]] рынка используются индикаторы, в расчетах которых используются входные данные, выдаваемые временными интервалами и сгруппированными на этих интервалах значениями котировок. Наиболее распространенная и общепринятая группировка котировок - в виде [[Японские свечи|свечей]] или баров. Выделяют 3 вида данных получаемых от свечной конфигурации или баров: цена, по которой был открыт период; цена, по которой период был закрыт; экстремальные значения данного временного периода. |
Более упрощенное представление колебаний котировок – это усреднение их по какому-либо одному выходному параметру с объединением таймфреймов в некий числовой ряд. Длину этого числового ряда принимают за период. | Более упрощенное представление колебаний котировок – это усреднение их по какому-либо одному выходному параметру с объединением таймфреймов в некий числовой ряд. Длину этого числового ряда принимают за период. | ||
| Строка 23: | Строка 23: | ||
Коэффициент, введенный в ее формулу выглядел следующим образом | Коэффициент, введенный в ее формулу выглядел следующим образом | ||
| − | [[Файл:FRAMA_100. | + | [[Файл:FRAMA_100.png]] |
Таким образом, при периоде n = 10 вес «первых» данных возрастал на 19%. | Таким образом, при периоде n = 10 вес «первых» данных возрастал на 19%. | ||
| − | Тушар Шонде один из первых, кто предложил включить в коэффициент скользящей средней -индикатор. В своем варианте скользящей средней VIDYA, он умножил коэффициент на «именной» индикатор СМО. Ввод такого множителя позволил кривой «прижиматься» к графику с ростом волатильности и «удаляьтся» с приходом на рынок движений в каком-то узком диапазоне цен (флэте). | + | Тушар Шонде один из первых, кто предложил включить в коэффициент [[Moving Averages|скользящей средней]] - индикатор. В своем варианте скользящей средней VIDYA, он умножил коэффициент на «именной» индикатор СМО. Ввод такого множителя позволил кривой «прижиматься» к графику с ростом волатильности и «удаляьтся» с приходом на рынок движений в каком-то узком диапазоне цен (флэте). |
По истечении трех лет, после Шонде, Кауфман рассчитал коэффициент более сложным образом через константы «быстрого» и « медленного» рынка. Скользящая средняя КАМА благодаря коэффициенту менялась от быстрого двухпериодного состояния до медленного 30 периодного. Величина изменения регулировалась, так называемым коэффициентом эффективности, выявлявшим «шум» рынка. Именно вариант Кауфмана получил большее распространения на рынке. | По истечении трех лет, после Шонде, Кауфман рассчитал коэффициент более сложным образом через константы «быстрого» и « медленного» рынка. Скользящая средняя КАМА благодаря коэффициенту менялась от быстрого двухпериодного состояния до медленного 30 периодного. Величина изменения регулировалась, так называемым коэффициентом эффективности, выявлявшим «шум» рынка. Именно вариант Кауфмана получил большее распространения на рынке. | ||
| Строка 33: | Строка 33: | ||
== Фракталы FRAMA == | == Фракталы FRAMA == | ||
| − | '''Предупреждение!''' Фракталы, используемые в расчетах FRAMA, не имеют ничего общего с фракталами Билла Вильямса, которые в свою очередь не имеют ничего общего с математическим понятием фрактала. | + | '''Предупреждение!''' [[Фракталы|Фракталы]], используемые в расчетах FRAMA, не имеют ничего общего с фракталами Билла Вильямса, которые в свою очередь не имеют ничего общего с математическим понятием фрактала. |
Фрактал в математике определяется как некое целое, части которого имеют ту же форму, что и само целое. То есть, соблюдается принцип «самоподобия». | Фрактал в математике определяется как некое целое, части которого имеют ту же форму, что и само целое. То есть, соблюдается принцип «самоподобия». | ||
| Строка 53: | Строка 53: | ||
Если мы имеем некое числовое множество, то в метрическом пространстве мы можем определить его фрактальную размерность с помощью мерных шаров некоего радиуса по формуле: | Если мы имеем некое числовое множество, то в метрическом пространстве мы можем определить его фрактальную размерность с помощью мерных шаров некоего радиуса по формуле: | ||
| − | [[Файл:FRAMA_101. | + | [[Файл:FRAMA_101.png]] |
в этой формуле N - количество шаров, радиусом равным ε которыми можно заполнить множество. | в этой формуле N - количество шаров, радиусом равным ε которыми можно заполнить множество. | ||
| − | Размерность фрактала равная единицы представляет собой прямую линию, размерность фрактала для плоскости равна 2. Согласно теории размерность фрактала может принимать дробные значения. Таким образом, мы можем благодаря размерности определить состояние котировок от тренда (прямой линии) до флэта (плоскости). | + | Размерность фрактала равная единицы представляет собой прямую линию, размерность фрактала для плоскости равна 2. Согласно теории размерность фрактала может принимать дробные значения. Таким образом, мы можем благодаря размерности определить состояние котировок от [[Тренд|тренда]] (прямой линии) до [[Флэт (Flat)|флэта]] (плоскости). |
Для этого берется период N. Условие для выбора одно - четность. Разбиваем период на две части N1,N2. В обеих частях этого периода находим экстремумы. Находим также экстремумы и для всего периода в целом. Они могут совпадать или не совпадать по значениям – это неважно. | Для этого берется период N. Условие для выбора одно - четность. Разбиваем период на две части N1,N2. В обеих частях этого периода находим экстремумы. Находим также экстремумы и для всего периода в целом. Они могут совпадать или не совпадать по значениям – это неважно. | ||
| Строка 65: | Строка 65: | ||
Формула размерности фрактала выглядит так: | Формула размерности фрактала выглядит так: | ||
| − | [[Файл:FRAMA_102. | + | [[Файл:FRAMA_102.png]] |
Если осуществить математически возможность взаимосвязи коэффициента скользящей средней к и размерности фрактала D, тогда можно говорить об адаптации выбранного нами периода под изменение состояния движения котировк. | Если осуществить математически возможность взаимосвязи коэффициента скользящей средней к и размерности фрактала D, тогда можно говорить об адаптации выбранного нами периода под изменение состояния движения котировк. | ||
| Строка 71: | Строка 71: | ||
Джон Эйлерс предложил установить такую связь через экспоненциальную функцию: | Джон Эйлерс предложил установить такую связь через экспоненциальную функцию: | ||
| − | [[Файл:FRAMA_103. | + | [[Файл:FRAMA_103.png]] |
В современном виде формула представляет собой «упрощенный вариант»: | В современном виде формула представляет собой «упрощенный вариант»: | ||
| − | [[Файл:FRAMA_104. | + | [[Файл:FRAMA_104.png]] |
Сам коэффициент, высчитанный по этой формуле, подставляется в формулу ЕМА | Сам коэффициент, высчитанный по этой формуле, подставляется в формулу ЕМА | ||
| Строка 93: | Строка 93: | ||
Продажи рекомендуется совершать после того, как свеча котировок закроется ниже кривой линии FRAMA. | Продажи рекомендуется совершать после того, как свеча котировок закроется ниже кривой линии FRAMA. | ||
| − | Стратегия подразумевает под собой реверсивное совершение сделок. Тогда, когда поступит противоположный сигнал, одновременно закрывается текущая позиция и открывается ей противоположная. Поэтому стопы в такой стратегии не практикуются. | + | Стратегия подразумевает под собой реверсивное совершение сделок. Тогда, когда поступит противоположный сигнал, одновременно закрывается текущая позиция и открывается ей противоположная. Поэтому [[Стоп-лосс|стопы]] в такой стратегии не практикуются. |
== Заключение == | == Заключение == | ||
Текущая версия на 13:59, 9 августа 2016
Фрактальная адаптивная скользящая средняя (FRAMA) - индикатор, адаптирующий свою скорость изменения исчисления, исходя из скорости изменения котировок.
Начало 90-х годов прошлого века означилось прорывом в области адаптаций рыночных областей значений анализируемых инструментов к соответствию динамики изменяющихся состояний рынка.
Для технического анализа рынка используются индикаторы, в расчетах которых используются входные данные, выдаваемые временными интервалами и сгруппированными на этих интервалах значениями котировок. Наиболее распространенная и общепринятая группировка котировок - в виде свечей или баров. Выделяют 3 вида данных получаемых от свечной конфигурации или баров: цена, по которой был открыт период; цена, по которой период был закрыт; экстремальные значения данного временного периода.
Более упрощенное представление колебаний котировок – это усреднение их по какому-либо одному выходному параметру с объединением таймфреймов в некий числовой ряд. Длину этого числового ряда принимают за период.
Но рынок не является периодической функцией, с помощью которой мы могли бы точно описать колебания котировок актива. Значения цен непредсказуемы и технический анализ неточен. Все это приводит к ошибкам прогнозов и, как следствие, к убыткам.
Вся проблема анализа числовых рядов котировок состоит в том, что получая новые котировки, усреднение происходит на периоде, где присутствуют еще старые котировки. Соответственно, сигналы или реакция кривой запаздывают. Уменьшением периода проблему запаздывания не решить. Возникнет множество сигналов, но мы, что называется, не будем видеть дальше своего носа, общая тенденция будет утеряна и, как следствие, большое количество из сигналов будет ложным.
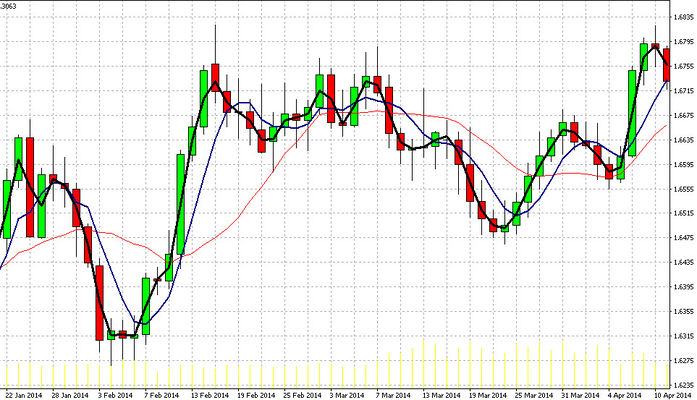
На рисунке разным цветом и толщиной изображены скользящие средние: скользящая средняя красного цвета имеет период равный 13, синего цвета скользящая средняя период равный 5, черным цветом обозначена скользящая средняя с наименьшим периодом 2.
Бороться с запаздыванием сигналов было решено с помощью введения в расчеты индикатора скользящей средней коэффициентов.
Первая в этой эволюции была экспоненциальная скользящая средняя. Обозначим формулу ЕМА, которая стала базовой для расчетов адаптационных скользящих средних.
ЕМА = к*Текущая цена+ (1-к)*ЕМАпред.значение
Коэффициент, введенный в ее формулу выглядел следующим образом
Таким образом, при периоде n = 10 вес «первых» данных возрастал на 19%.
Тушар Шонде один из первых, кто предложил включить в коэффициент скользящей средней - индикатор. В своем варианте скользящей средней VIDYA, он умножил коэффициент на «именной» индикатор СМО. Ввод такого множителя позволил кривой «прижиматься» к графику с ростом волатильности и «удаляьтся» с приходом на рынок движений в каком-то узком диапазоне цен (флэте).
По истечении трех лет, после Шонде, Кауфман рассчитал коэффициент более сложным образом через константы «быстрого» и « медленного» рынка. Скользящая средняя КАМА благодаря коэффициенту менялась от быстрого двухпериодного состояния до медленного 30 периодного. Величина изменения регулировалась, так называемым коэффициентом эффективности, выявлявшим «шум» рынка. Именно вариант Кауфмана получил большее распространения на рынке.
Содержание
Фракталы FRAMA
Предупреждение! Фракталы, используемые в расчетах FRAMA, не имеют ничего общего с фракталами Билла Вильямса, которые в свою очередь не имеют ничего общего с математическим понятием фрактала.
Фрактал в математике определяется как некое целое, части которого имеют ту же форму, что и само целое. То есть, соблюдается принцип «самоподобия».
Например - снежинки или кровеносная система бронхи человека и животного. Лучшим визуальным представлением фрактала, является голографическое изображение. Если его разбить, каждый кусочек будет содержать не фрагмент, а исходное изображение в целом.
Колебания котировок также самоподобны, переключая таймфреймы, мы видим возможность построения тех же треугольников и трендовых линий, наблюдаем и находим работающие различные комбинации свечей, которые описаны в «свечном» техническом анализе. Есть целый практикум по поиску и сравнений ситуаций, когда поведение цен в историческом прошлом идентично «сегодняшнему дню».
Присутствие фракталов на рынке обнаружил и описал французский и американский математик Мандельброт Бенуа. Для этого он исследовал столетнюю статистику цен на хлопок. Однако, это свойство являлось описательным для рынка, но никакого прогностического значения не имело, пока технический аналитик Джон Эйлерс не нашел ему достойное применение.
Основная концепция и формула FRAMA
Если брать упрощенно, изыскания по созданию, или правильней сказать адаптации, скользящей средней сводятся к тому, чтобы найти коэффициент к для формулы скользящей средней, которая является базовой для всех адаптивных скользящих (АМА). Это формула ЕМА и она описана выше.
При чем, коэффициент должен предусматривать «смену режимов» для анализа котировок при изменении динамики поведения котировок.
Джон Эйлерс решил данный вопрос, когда применил понятие определение размерности фракталов.
Если мы имеем некое числовое множество, то в метрическом пространстве мы можем определить его фрактальную размерность с помощью мерных шаров некоего радиуса по формуле:
в этой формуле N - количество шаров, радиусом равным ε которыми можно заполнить множество.
Размерность фрактала равная единицы представляет собой прямую линию, размерность фрактала для плоскости равна 2. Согласно теории размерность фрактала может принимать дробные значения. Таким образом, мы можем благодаря размерности определить состояние котировок от тренда (прямой линии) до флэта (плоскости).
Для этого берется период N. Условие для выбора одно - четность. Разбиваем период на две части N1,N2. В обеих частях этого периода находим экстремумы. Находим также экстремумы и для всего периода в целом. Они могут совпадать или не совпадать по значениям – это неважно.
Нам важно рассчитать размерность фрактала. Она рассчитывается через соотношение логарифмов диапазонов периода. Найдем их - это разности трех экстремумов : первой части периода Диапазон Д1 = Максимум 1 – Минимум 1, аналогично второй Д2 = Максимум 2 - Минимум 2 и общий обозначим До = Максимум всего периода – Минимум всего периода.
Формула размерности фрактала выглядит так:
Если осуществить математически возможность взаимосвязи коэффициента скользящей средней к и размерности фрактала D, тогда можно говорить об адаптации выбранного нами периода под изменение состояния движения котировк.
Джон Эйлерс предложил установить такую связь через экспоненциальную функцию:
В современном виде формула представляет собой «упрощенный вариант»:
Сам коэффициент, высчитанный по этой формуле, подставляется в формулу ЕМА
FRAMA = к*Цена закрытия +(1-к) FRAMA предыдущее значение
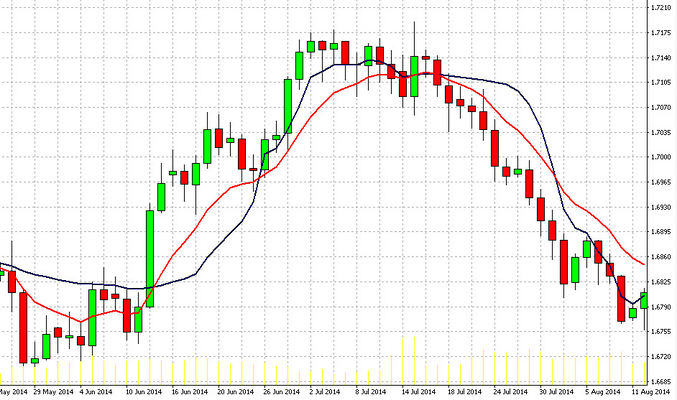
На рисунке изображена скользящая средняя экспоненциального расчета и FRAMA
Стратегия работы с использованием FRAMA
Хотя коэффициент у FRAMA вычисляется довольно необычным способом, это не исключает того факта, что индикатор является скользящей средней. Соответственно, весь набор правил, который справедлив для работы со скользящими средними, применим и на этой стратегии. Одну особенность надо отметить - кривая в силу учета, при своем вычислении динамики изменения рыночных данных, сама разворачивается за ценой. Поэтому иногда в литературе описаны способы входа словами-«при развороте скользящей средней…». Мы же все-таки будем опираться на классическое толкование сигналов.
Покупки рекомендуется совершать после того, как котировки выбранного таймфрейма превысят кривую линию FRAMA.
Продажи рекомендуется совершать после того, как свеча котировок закроется ниже кривой линии FRAMA.
Стратегия подразумевает под собой реверсивное совершение сделок. Тогда, когда поступит противоположный сигнал, одновременно закрывается текущая позиция и открывается ей противоположная. Поэтому стопы в такой стратегии не практикуются.
Заключение
Смысл поисков и прикладываемых усилий по адаптации индикаторов состоит в том, чтобы улучшить правильность прогнозов цен и, как следствие, результаты торговли. На момент написания статьи не было обнаружено ни одного индикатора со стопроцентной результативностью. Поэтому, принимая решение об использовании в торговле того или иного технического инструмента, а в особенности замены своей старой стратегии на «вновь открытую», стоит озаботиться о тщательных тестах. Помните пословицу - «Лучшее - враг хорошего».