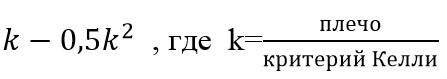Admin (обсуждение | вклад) (→Недостатки формулы Келли) |
Lika (обсуждение | вклад) |
||
| Строка 1: | Строка 1: | ||
Джон Лари Келли в 1956 году предложил тактику определения ставок в азартной игре. Пользуясь математической формулой автора профессиональный игрок (беттор) определял размер конкретной ставки на спортивное событие. В расчет включался общий размер средств игрока, вероятность выигрыша по версии букмекера и беттора. | Джон Лари Келли в 1956 году предложил тактику определения ставок в азартной игре. Пользуясь математической формулой автора профессиональный игрок (беттор) определял размер конкретной ставки на спортивное событие. В расчет включался общий размер средств игрока, вероятность выигрыша по версии букмекера и беттора. | ||
| − | Инвестиционные фонды адаптировали принципы критерия Келли для фондовых рынков. При правильном определении вероятности прибыли по каждой сделке или отдельному портфелю | + | Инвестиционные фонды адаптировали принципы критерия Келли для фондовых рынков. При правильном определении вероятности прибыли по каждой сделке или отдельному портфелю с помощью формул происходила диверсифицикация капитала, самым оптимальным образом максимизируя прибыль. |
Как применять расчеты для рынков первым показал Гарри Марковиц, известный американский экономист и портфельный инвестор, используя критерий в рамках собственной теории инвестирования. На основании алгоритма ученого трейдеры масштабировали расчеты формулы Келли применительно ко всем типам рынков. | Как применять расчеты для рынков первым показал Гарри Марковиц, известный американский экономист и портфельный инвестор, используя критерий в рамках собственной теории инвестирования. На основании алгоритма ученого трейдеры масштабировали расчеты формулы Келли применительно ко всем типам рынков. | ||
| Строка 7: | Строка 7: | ||
== Расчет критерия Келли == | == Расчет критерия Келли == | ||
| − | Классическая формула в изложении автора | + | Классическая формула в изложении автора выглядит следующим образом: |
[[File:risk managment (43).jpg]] | [[File:risk managment (43).jpg]] | ||
| Строка 21: | Строка 21: | ||
Размер торгового капитала = Вероятность профита – Вероятность убытка. | Размер торгового капитала = Вероятность профита – Вероятность убытка. | ||
| − | Трейдеры принимают за вероятность профита математическое ожидание или | + | Трейдеры принимают за вероятность профита математическое ожидание или вычисляют простое соотношение прибыльных сделок от их общего числа. |
Если доля прибыльных сделок составляет 60%, вероятность убыточных будет равна 40%. | Если доля прибыльных сделок составляет 60%, вероятность убыточных будет равна 40%. | ||
| + | |||
Тогда получим: | Тогда получим: | ||
| − | Размер торгового капитала = 60%- 40%= 20%. | + | Размер торгового капитала = 60% - 40% = 20%. |
| − | Оптимальный размер депозита, выделяемого на валютные спекуляции при 60% положительных сделок (на истории) не должен превышать 20%. | + | Оптимальный размер депозита, выделяемого на валютные спекуляции при 60% положительных сделок (на истории), не должен превышать 20%. |
== Положительные свойства применения критерия Келли == | == Положительные свойства применения критерия Келли == | ||
| − | При однозначно определенном положительном математическом ожидании торговой системы | + | При однозначно определенном положительном математическом ожидании торговой системы критерий Келли позволяет: |
| + | |||
* просчитать или задать траекторию увеличения капитала | * просчитать или задать траекторию увеличения капитала | ||
* определить точное количество сделок (серию) для достижения заданной теоретической доходности | * определить точное количество сделок (серию) для достижения заданной теоретической доходности | ||
| − | Любая торговая система стремится к убытку с течением времени. Этого не избежать | + | Любая торговая система стремится к убытку с течением времени. Этого не избежать вне зависимости от затраченного времени подбора «идеальных» параметров индикаторов, правил и длительности тестов. |
Если трейдер знает примерную продолжительность жизни стратегии (выраженную в сделках), рассчитав траекторию капитала по тестовым данным, можно контролировать расхождение с реальными значениями роста прибыли, чтобы вовремя определить отказ работоспособности. | Если трейдер знает примерную продолжительность жизни стратегии (выраженную в сделках), рассчитав траекторию капитала по тестовым данным, можно контролировать расхождение с реальными значениями роста прибыли, чтобы вовремя определить отказ работоспособности. | ||
| Строка 64: | Строка 66: | ||
Серия рыночных сделок содержит различный финансовый результат, что приводит к погрешности при вычислении среднего выигрыша и проигрыша (в азартных играх это фиксированное и заранее известное значение). | Серия рыночных сделок содержит различный финансовый результат, что приводит к погрешности при вычислении среднего выигрыша и проигрыша (в азартных играх это фиксированное и заранее известное значение). | ||
| − | Ральф Винс, который ввел понятие оптимального f на рынки, предложил делать поправку вычисляемого критерия Келли на соотношение максимальной убыточной сделки W (в пунктах) к значению [[Котировка|котировки]] P | + | Ральф Винс, который ввел понятие оптимального f на рынки, предложил делать поправку вычисляемого критерия Келли на соотношение максимальной убыточной сделки W (в пунктах) к значению [[Котировка|котировки]] P. |
Расчеты производятся как по отдельным, так и средним значениям серии сделок. | Расчеты производятся как по отдельным, так и средним значениям серии сделок. | ||
| Строка 72: | Строка 74: | ||
1. Критерий Келли не учитывает количество убыточных сделок подряд. Серии убытков, следующие одна за другой с малым перерывом, уничтожат депозит, несмотря на расчеты. | 1. Критерий Келли не учитывает количество убыточных сделок подряд. Серии убытков, следующие одна за другой с малым перерывом, уничтожат депозит, несмотря на расчеты. | ||
| − | 2. Формула не учитывает максимальную просадку (системы или единичной сделки). Трейдер не сможет восстановить депозит | + | 2. Формула не учитывает максимальную просадку (системы или единичной сделки). Трейдер не сможет восстановить депозит после нескольких крупных убытков. |
| − | 3. Формула не применима внутри дня, так как предполагает планирование и расчет критерия по каждой | + | 3. Формула не применима внутри дня, так как предполагает планирование и расчет критерия по каждой сделке. |
| − | 4. Надежность расчетов критерия зависит от точности входных данных. Они могут быть получены из реальной истории торгов или тестов. Если данные недостоверны ( | + | 4. Надежность расчетов критерия зависит от точности входных данных. Они могут быть получены из реальной истории торгов или тестов. Если данные недостоверны (малый размер выборки, неточные тесты), это приведет к завышению размера [[Плечо|плеча]]. В таком случае депозит ждет «яма для жадных». |
[[Category:Термины]] | [[Category:Термины]] | ||
[[Category:Мани-менеджмент]] | [[Category:Мани-менеджмент]] | ||
Версия 11:35, 14 ноября 2017
Джон Лари Келли в 1956 году предложил тактику определения ставок в азартной игре. Пользуясь математической формулой автора профессиональный игрок (беттор) определял размер конкретной ставки на спортивное событие. В расчет включался общий размер средств игрока, вероятность выигрыша по версии букмекера и беттора.
Инвестиционные фонды адаптировали принципы критерия Келли для фондовых рынков. При правильном определении вероятности прибыли по каждой сделке или отдельному портфелю с помощью формул происходила диверсифицикация капитала, самым оптимальным образом максимизируя прибыль.
Как применять расчеты для рынков первым показал Гарри Марковиц, известный американский экономист и портфельный инвестор, используя критерий в рамках собственной теории инвестирования. На основании алгоритма ученого трейдеры масштабировали расчеты формулы Келли применительно ко всем типам рынков.
Содержание
Расчет критерия Келли
Классическая формула в изложении автора выглядит следующим образом:
Полученный результат всегда находится в пределах от 0 до 1, размер ставки определяется умножением всей игровой суммы, называемой банком, на это значение.
На рынке Форекс чаще всего используют видоизмененную формулу:
Справедливо отметить, что трейдеры не обладают надежными средствами по вычислению вероятности прибыли или убытка, поэтому часто их приравнивают, сводя формулу к простому выражению
Размер торгового капитала = Вероятность профита – Вероятность убытка.
Трейдеры принимают за вероятность профита математическое ожидание или вычисляют простое соотношение прибыльных сделок от их общего числа.
Если доля прибыльных сделок составляет 60%, вероятность убыточных будет равна 40%.
Тогда получим:
Размер торгового капитала = 60% - 40% = 20%.
Оптимальный размер депозита, выделяемого на валютные спекуляции при 60% положительных сделок (на истории), не должен превышать 20%.
Положительные свойства применения критерия Келли
При однозначно определенном положительном математическом ожидании торговой системы критерий Келли позволяет:
- просчитать или задать траекторию увеличения капитала
- определить точное количество сделок (серию) для достижения заданной теоретической доходности
Любая торговая система стремится к убытку с течением времени. Этого не избежать вне зависимости от затраченного времени подбора «идеальных» параметров индикаторов, правил и длительности тестов.
Если трейдер знает примерную продолжительность жизни стратегии (выраженную в сделках), рассчитав траекторию капитала по тестовым данным, можно контролировать расхождение с реальными значениями роста прибыли, чтобы вовремя определить отказ работоспособности.
Графическое отображение свойств критерия Келли
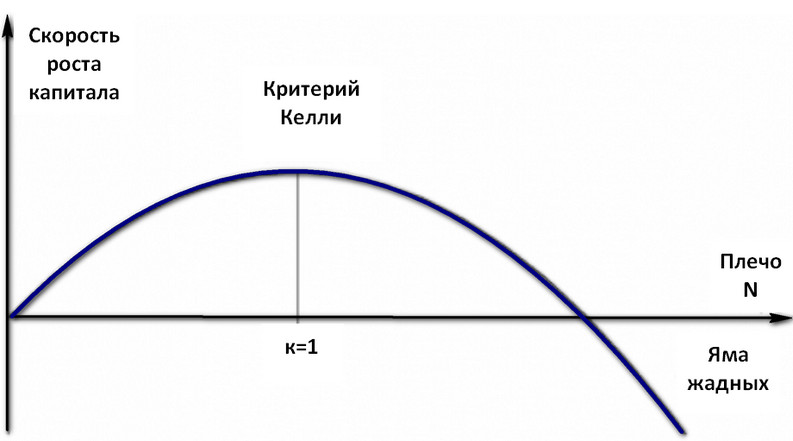
Критерий Келли выражают на графике функциональной зависимости относительного роста капитала от размера плеча. Зависимость определена уравнением:
На графике мы получим параболу, пик которой приходится на критерий Келли равный 1 (скорость роста капитала пропорциональна плечу).
На рисунке наглядно показано, как неограниченный рост плеча приводит к уничтожению трейдерского депозита. Отрицательная область была названа – «Ямой для жадных».
Практические выводы по критерию Келли
Перебор плеча (выход за точку к=1 в параболе) всегда будет вносить отрицательный вклад в любую стратегию с положительным матожиданием. Так как оценка прибыльности стратегии носит вероятностный характер, плечо лучше выбрать несколько ниже просчитанного критерия Келли.
На практике трейдеры пользуются понятием «критерий полу-Келли» - это позволяет получать ¾ запланированного дохода, но снижает вдвое разброс убытков и прибылей (волатильности торговых результатов.
Взаимосвязь критерия Келли с оптимальным f
Несмотря на адаптацию формулы Келли для финансовых, фондовых и товарных рынков, она учитывает два исхода – выигрыш и проигрыш ставки. (+1 или-1).
Серия рыночных сделок содержит различный финансовый результат, что приводит к погрешности при вычислении среднего выигрыша и проигрыша (в азартных играх это фиксированное и заранее известное значение).
Ральф Винс, который ввел понятие оптимального f на рынки, предложил делать поправку вычисляемого критерия Келли на соотношение максимальной убыточной сделки W (в пунктах) к значению котировки P.
Расчеты производятся как по отдельным, так и средним значениям серии сделок.
Недостатки формулы Келли
1. Критерий Келли не учитывает количество убыточных сделок подряд. Серии убытков, следующие одна за другой с малым перерывом, уничтожат депозит, несмотря на расчеты.
2. Формула не учитывает максимальную просадку (системы или единичной сделки). Трейдер не сможет восстановить депозит после нескольких крупных убытков.
3. Формула не применима внутри дня, так как предполагает планирование и расчет критерия по каждой сделке.
4. Надежность расчетов критерия зависит от точности входных данных. Они могут быть получены из реальной истории торгов или тестов. Если данные недостоверны (малый размер выборки, неточные тесты), это приведет к завышению размера плеча. В таком случае депозит ждет «яма для жадных».