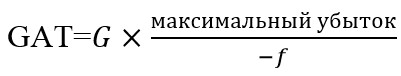Admin (обсуждение | вклад) (→Практическое применения средней геометрической сделки) |
Lika (обсуждение | вклад) |
||
| Строка 1: | Строка 1: | ||
| − | Средняя геометрическая сделка – это аналог средней сделки, для оценки систем с [[Реинвестирование|реинвестированием]]. В случае постоянного увеличения депозита | + | Средняя геометрическая сделка – это аналог средней сделки, для оценки систем с [[Реинвестирование|реинвестированием]]. В случае постоянного увеличения депозита арифметически подсчитанная средняя прибыль системы не будет обладать адекватной оценкой. |
Среднее значение необходимо для контроля и планирования доходности торговой системы, а также общей оценки введенных тактических изменений по риск менеджменту. | Среднее значение необходимо для контроля и планирования доходности торговой системы, а также общей оценки введенных тактических изменений по риск менеджменту. | ||
| Строка 7: | Строка 7: | ||
== Формула средней геометрической сделки == | == Формула средней геометрической сделки == | ||
| − | Формула была предложена Ральфом Винсом | + | Формула была предложена Ральфом Винсом и вычисляется с помощью среднего геометрического прибыли и оптимального f, величинам, относящимся к авторским изысканиям. |
[[File:risk managment (3).jpg]] | [[File:risk managment (3).jpg]] | ||
| − | , где G считают по формуле G= Среднее геометрическое прибыли -1 | + | , где G считают по формуле G = Среднее геометрическое прибыли -1 |
| + | |||
Среднее геометрическое прибыли должно быть определено ранее, как обязательный критерий проверки возможности применения реинвестирования в стратегии: | Среднее геометрическое прибыли должно быть определено ранее, как обязательный критерий проверки возможности применения реинвестирования в стратегии: | ||
| Строка 18: | Строка 19: | ||
Чистая прибыль возводится в степень, обратную количеству сделок, за которые она получена. Показатель должен быть выше 1, иначе реинвестирование, как и формула GAT не имеет смысла. | Чистая прибыль возводится в степень, обратную количеству сделок, за которые она получена. Показатель должен быть выше 1, иначе реинвестирование, как и формула GAT не имеет смысла. | ||
| − | Оптимальное f определяется путем перебора значений в числовом промежутке от 0 до 1 с шагом 0,01, чтобы Максимальная прибыль в выражении ниже | + | Оптимальное f определяется путем перебора значений в числовом промежутке от 0 до 1 с шагом 0,01, чтобы Максимальная прибыль в выражении ниже была оптимальной: |
[[File:risk managment (45).jpg]] | [[File:risk managment (45).jpg]] | ||
| − | Сделав промежуточные расчеты, подставив полученные | + | Сделав промежуточные расчеты, подставив полученные значения в выражение GAT (средней геометрической сделки), получают положительные результаты, так как по замыслу автора минус перед f компенсирует отрицательный знак убытка (по мнению Винса – убыток всегда отрицательное число). |
== Практическое применения средней геометрической сделки == | == Практическое применения средней геометрической сделки == | ||
| − | Значения средней геометрической сделки | + | Значения средней геометрической сделки представляют собой проценты [[Математическое ожидание прибыли|матожидания]]. Например, 1.03 – это матожидание системы в 3%. Таким образом трейдер может контролировать «производительность» системы при постоянном увеличении [[Лоты|торгового лота]], несмотря на изменяющийся арифметический результат средней сделки. |
[[Category:Термины]] | [[Category:Термины]] | ||
[[Category:Мани-менеджмент]] | [[Category:Мани-менеджмент]] | ||
Версия 06:00, 17 ноября 2017
Средняя геометрическая сделка – это аналог средней сделки, для оценки систем с реинвестированием. В случае постоянного увеличения депозита арифметически подсчитанная средняя прибыль системы не будет обладать адекватной оценкой.
Среднее значение необходимо для контроля и планирования доходности торговой системы, а также общей оценки введенных тактических изменений по риск менеджменту.
Содержание
Формула средней геометрической сделки
Формула была предложена Ральфом Винсом и вычисляется с помощью среднего геометрического прибыли и оптимального f, величинам, относящимся к авторским изысканиям.
, где G считают по формуле G = Среднее геометрическое прибыли -1
Среднее геометрическое прибыли должно быть определено ранее, как обязательный критерий проверки возможности применения реинвестирования в стратегии:
Чистая прибыль возводится в степень, обратную количеству сделок, за которые она получена. Показатель должен быть выше 1, иначе реинвестирование, как и формула GAT не имеет смысла.
Оптимальное f определяется путем перебора значений в числовом промежутке от 0 до 1 с шагом 0,01, чтобы Максимальная прибыль в выражении ниже была оптимальной:
Сделав промежуточные расчеты, подставив полученные значения в выражение GAT (средней геометрической сделки), получают положительные результаты, так как по замыслу автора минус перед f компенсирует отрицательный знак убытка (по мнению Винса – убыток всегда отрицательное число).
Практическое применения средней геометрической сделки
Значения средней геометрической сделки представляют собой проценты матожидания. Например, 1.03 – это матожидание системы в 3%. Таким образом трейдер может контролировать «производительность» системы при постоянном увеличении торгового лота, несмотря на изменяющийся арифметический результат средней сделки.