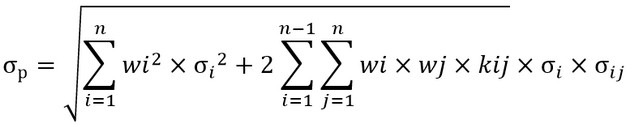Admin (обсуждение | вклад) |
Lika (обсуждение | вклад) |
||
| (не показаны 2 промежуточных версий 2 участников) | |||
| Строка 1: | Строка 1: | ||
| − | Методика отбора рыночных активов ([[Валютные пары|валюта]], товары, ценные бумаги) | + | Методика отбора рыночных активов ([[Валютные пары|валюта]], товары, [[Рынок ценных бумаг и производных финансовых инструментов|ценные бумаги]]) на основе заданного соотношения риска и доходности определяется моделью Марковица. |
Формула названа по имени лауреата Нобелевской премии по экономики Гарри Марковица, идеи которого легли в основу модели управления инвестиционными портфелями. | Формула названа по имени лауреата Нобелевской премии по экономики Гарри Марковица, идеи которого легли в основу модели управления инвестиционными портфелями. | ||
| − | Суть управления была найдена в ходе написания ученым докторской диссертации по инвестиционной экономике. Выдержки из нее были опубликованы в статье для «Финансового Журнала», где оптимальный набор инструментов задавался четко сформулированными правилами. Более детально принципы были изложены выпущенной в конце 50-х книге – «Выбор портфеля: эффективная [[диверсификация]] инвестиций». | + | Суть управления была найдена в ходе написания ученым докторской диссертации по инвестиционной экономике. Выдержки из нее были опубликованы в статье для «Финансового Журнала», где оптимальный набор инструментов задавался четко сформулированными правилами. Более детально принципы были изложены в выпущенной в конце 50-х книге – «Выбор портфеля: эффективная [[диверсификация]] инвестиций». |
__TOC__ | __TOC__ | ||
| Строка 14: | Строка 14: | ||
1. Наилучшая диверсификация у инструментов с отрицательным коэффициентом [[Корреляция|корреляции]]. | 1. Наилучшая диверсификация у инструментов с отрицательным коэффициентом [[Корреляция|корреляции]]. | ||
| − | 2. Выбор инструмента должен происходить по параметру низкого риска, а не | + | 2. Выбор инструмента должен происходить по параметру низкого риска, а не высокодоходности. |
3. Стратегия считается неэффективной, если ее доходность можно увеличить без роста риска или наоборот, уменьшить риск без падения прибыльности. | 3. Стратегия считается неэффективной, если ее доходность можно увеличить без роста риска или наоборот, уменьшить риск без падения прибыльности. | ||
| − | Опираясь на последний принцип можно подобрать эффективные инструменты (портфели | + | Опираясь на последний принцип можно подобрать эффективные инструменты (портфели стратегий), у которых прибыль уменьшается при увеличении риска и наоборот. |
Ученый строил график зависимости нормы прибыли от риска и располагал такие портфели за границей эффективности: | Ученый строил график зависимости нормы прибыли от риска и располагал такие портфели за границей эффективности: | ||
| Строка 23: | Строка 23: | ||
[[File:risk managment (35).jpg]] | [[File:risk managment (35).jpg]] | ||
| − | Это графическое отображение, как увеличение риска | + | Это графическое отображение, как увеличение риска вызывает рост прибыли. При этом Марковиц опирается на некие предполагаемые доходности (отдачу) инструментов в будущем. Трейдеры обычно заменяют их тестовыми значениями торговых систем. |
== Формула модели Макровица == | == Формула модели Макровица == | ||
| Строка 31: | Строка 31: | ||
[[File:risk managment (20).jpg]] | [[File:risk managment (20).jpg]] | ||
| − | , где r – доходность, полученная в ходе тестов, называемая ожидаемой, взятая по отдельной стратегии или портфелю в целом из которой вычитается средняя доходность за тестовый период n | + | , где r – доходность, полученная в ходе тестов, называемая ожидаемой, взятая по отдельной стратегии или портфелю в целом, из которой вычитается средняя доходность за тестовый период n. |
| − | Если в портфеле несколько инструментов, то при расчете риска используется понятие их доли w, корреляции k и ковариации V между | + | Если в портфеле несколько инструментов, то при расчете риска используется понятие их доли w, корреляции k и ковариации V между ними. |
Риск портфеля по Марковицу: | Риск портфеля по Марковицу: | ||
| Строка 39: | Строка 39: | ||
[[File:risk managment (9).jpg]] | [[File:risk managment (9).jpg]] | ||
| − | , где i и j индексы обозначающие разные инструменты в одном портфеле. Подставляя ковариацию получим: | + | , где i и j индексы, обозначающие разные инструменты в одном портфеле. Подставляя ковариацию получим: |
[[File:risk managment (11).jpg]] | [[File:risk managment (11).jpg]] | ||
| Строка 58: | Строка 58: | ||
== Достоинства и недостатки практического применения модели == | == Достоинства и недостатки практического применения модели == | ||
| − | Модель подходит для рынка акций, предполагающего непрерывных рост актива и чувствительна к резким изменениям стоимости портфеля (волатильности результатов). | + | Модель подходит для рынка акций, предполагающего непрерывных рост актива, и чувствительна к резким изменениям стоимости портфеля ([[Волатильность|волатильности]] результатов). |
| − | Коэффициент корреляции между инструментами не является константой, постоянно изменяется требует пересчета. Расчеты основываются на предполагаемой доходности, основанной на вероятностном исчислении. | + | |
| + | Коэффициент корреляции между инструментами не является константой, постоянно изменяется и требует пересчета. Расчеты основываются на предполагаемой доходности, основанной на вероятностном исчислении. | ||
[[Category:Термины]] | [[Category:Термины]] | ||
| + | [[Category:Мани-менеджмент]] | ||
Текущая версия на 12:21, 18 ноября 2017
Методика отбора рыночных активов (валюта, товары, ценные бумаги) на основе заданного соотношения риска и доходности определяется моделью Марковица.
Формула названа по имени лауреата Нобелевской премии по экономики Гарри Марковица, идеи которого легли в основу модели управления инвестиционными портфелями.
Суть управления была найдена в ходе написания ученым докторской диссертации по инвестиционной экономике. Выдержки из нее были опубликованы в статье для «Финансового Журнала», где оптимальный набор инструментов задавался четко сформулированными правилами. Более детально принципы были изложены в выпущенной в конце 50-х книге – «Выбор портфеля: эффективная диверсификация инвестиций».
Содержание
Допущения теории управления портфелем по модели Марковица
Гарри Марковиц выводил модель, основываясь на предположении, что существует множество работоспособных стратегий, применимых для различных активов с прибыльным финансовым результатом.
Предполагалось, что трейдер будет подбирать конкретные инструменты и стратегии исходя из следующих принципов:
1. Наилучшая диверсификация у инструментов с отрицательным коэффициентом корреляции. 2. Выбор инструмента должен происходить по параметру низкого риска, а не высокодоходности. 3. Стратегия считается неэффективной, если ее доходность можно увеличить без роста риска или наоборот, уменьшить риск без падения прибыльности.
Опираясь на последний принцип можно подобрать эффективные инструменты (портфели стратегий), у которых прибыль уменьшается при увеличении риска и наоборот.
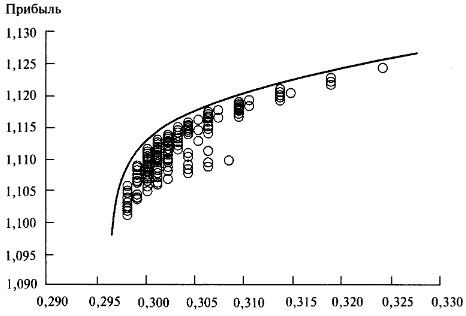
Ученый строил график зависимости нормы прибыли от риска и располагал такие портфели за границей эффективности:
Это графическое отображение, как увеличение риска вызывает рост прибыли. При этом Марковиц опирается на некие предполагаемые доходности (отдачу) инструментов в будущем. Трейдеры обычно заменяют их тестовыми значениями торговых систем.
Формула модели Макровица
Если у трейдера имеются тесты стратегий, портфели акций с предполагаемой доходностью или реальные результаты торгов, по каждому из них он может определить ее среднеквадратичное отклонение:
, где r – доходность, полученная в ходе тестов, называемая ожидаемой, взятая по отдельной стратегии или портфелю в целом, из которой вычитается средняя доходность за тестовый период n.
Если в портфеле несколько инструментов, то при расчете риска используется понятие их доли w, корреляции k и ковариации V между ними.
Риск портфеля по Марковицу:
, где i и j индексы, обозначающие разные инструменты в одном портфеле. Подставляя ковариацию получим:
Решение состоит в поиске минимального риска для портфеля и максимальной доходности, которое ограничено следующими тремя условиями:
1. Доли актива w должны быть положительными 2. Сумма долей активов равна 1(100%)
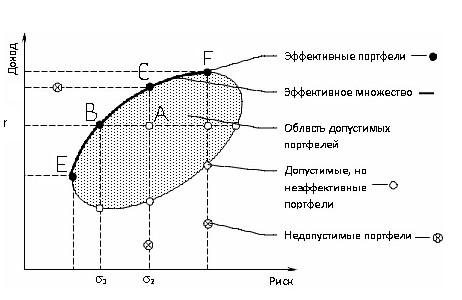
Графически эти решения можно отобразить в виде двух экспонент:
Эффективные стратегии по Марковицу – это системы с соотношением риск/доходность, попадающие на границу эффективности точки ABC и D. Конкретный выбор остается за трейдерами, опираясь на значение прибыли кто-то предпочтет более агрессивный трейдинг, иные выберут меньший риск.
Достоинства и недостатки практического применения модели
Модель подходит для рынка акций, предполагающего непрерывных рост актива, и чувствительна к резким изменениям стоимости портфеля (волатильности результатов).
Коэффициент корреляции между инструментами не является константой, постоянно изменяется и требует пересчета. Расчеты основываются на предполагаемой доходности, основанной на вероятностном исчислении.